Probabilistic machine learning

Unlike other methods probabilistic machine learning is based on one consistent principle which is used throughout the entire inference procedure. Probabilistic methods approach inference of latent variables, model coefficients, nuisance parameters and model order essentially by applying Bayesian Theory. Hence we may treat all unknown variables identically which is mathematically nice. For computational reasons a fully probabilistic model might not be feasible. In such situations we have to use approximations. Obviously for a methodology that has to stand the test in an empirical discipline, a mathematical consistency argument is not too convincing. So why should one use probabilistic methods?

Advantages of probabilistic models

• Fully probabilistic models avoid "black box" characteristics. We may instantiate arbitrary sets of variables and for diagnosis purposes infer the distributions over (or expectations of) other variables of interest and thus obtain some insight how we obtain a particular decision.
• Using a probabilistic model is relatively easy. Inference (if properly implemented) should be insensitive to the setting of all "fiddle parameters" and will thus provide results that are close to optimal. An example that relies on this property is adaptive inference which I have used for our adaptive classification.
• Probabilistic models provide means for intelligent sensor fusion which allows e.g. to combine information that is known with different certainty.

Disadvantages of probabilistic models

• Inference of fully probabilistic models can be slow.
• Inferring probabilistic models inevitably requires to model distributions. Sometimes this can be more than we are asked for.

Bayesian sensor fusion

The basic idea of Bayesian sensor fusion is to take uncertainty of information into account. In machine learning the seminal papers were those by (MacKay 1992) who discussed the effects of model uncertainty. In (Wright 1999) these ideas were later extended to input uncertainty. Related ideas have been used by (Dellaportas & Stephens 1995), who discuss models for errors in observables. I got interested in these issues in the context of hierarchical models where model parameters of a feature extraction stage are used for diagnosis or segmentation purposes. Such models are e.g. used for sleep analysis or also in the context of BCI. In a Bayesian sense these features are latent variables and should be treated as such. Again this is a consistency argument which has to be examined for its practical relevance.

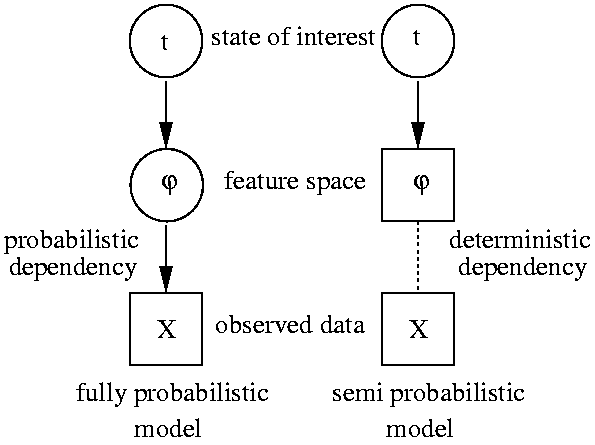In order to obtain a hierarchical model that does sensor fusion we simply regard the feature extraction stage as latent space and integrate (marginalize) over all uncertainties. The left figure compares a sensor fusing DAG with current practice in many applications of probabilistic modeling that regard extracted features as observations. I reported on a first attempt to approach this problem in (Sykacek 1999) which is in more detail described in section 4 in my Ph.D. thesis.

In order to see that a latent feature space has practical advantages, we consider a very simple case where two sensors are fused in a naive Bayes manner to predict the posterior probability in a two class problem. 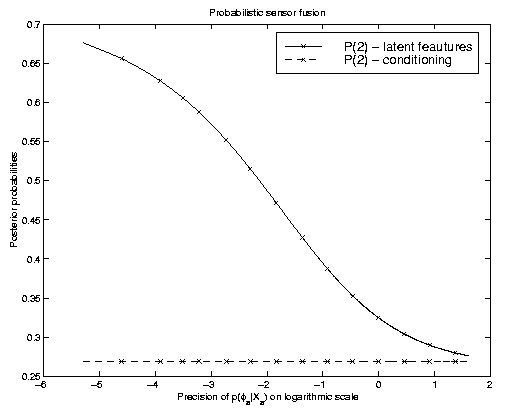The model is similar to the one in the graph used above, however with two latent feature stages that are, conditional on the state of interest t, assumed to be independent. The plot on the right illustrates the effect of knowing one of the latent features with varying precision. Conditioning on a best estimate results obviously in probabilities that are independent of the precision. We hence obtain a flat line with a probability of class "2" of about 0.27. Marginalization changes this probability. Depending on how much the uncertainties differ, we can, as is illustrated in this figure, also obtain different predicted states. We may thus expect to improve in such cases where the precision of the distributions in the latent feature space varies. We have successfully applied a HMM based latent feature space model to classification of segments of multi sensor time series. Such problems arise in clinical diagnosis (sleep classification) and in the context of brain computer interfaces (BCI). A MCMC implementation and evaluation on synthetic and BCI data has been published in (Sykacek & Roberts 2002 a). This work was also the topic of a talk I gave at the NCRG in Aston in July 2002. A pdf version of the slides being available here. Recently (Beal et al. 2002) have applied similar ideas to sensor fusion of audio and video data.

Adaptive classification based on variational Kalman filtering

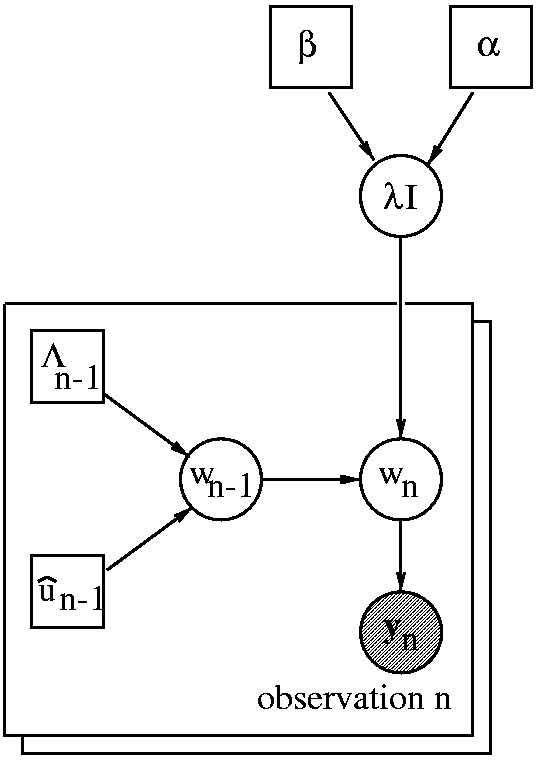
The image on the right shows a directed acyclic graph of our BCI classifier. Every time instance n represents a second of EEG and the corresponding cognitive state. At instance n, we are given a distribution over the parameter vector w_n-1 a new observation y_n. Assuming a two state BCI (e.g. we want to discriminate between cortical activity in the left and right motor cortex), y_n ∈ [0,1] and the BCI classifier predicts the probability P(y_n|D). We use D to denote all past observations including previous sessions. Data D results in a Gaussian distribution over the previous parameter p(w_n-1|D) which has mean û_n-1 and precision matrix Λ_n-1. As soon as we observe y_n we can update the distribution to obtain p(w_n-1|D, y_n). The hyper parameter λ can be regarded as a forgetting factor that controls the amount of tracking of the algorithm. Rather than setting its value directly, we use a hierarchical setup. We specify a Gamma prior p(λ|α, β) and infer the posterior distribution p(λ|y_n-N,...y_n-1,α, β). This assumes a stationary adaptation rate λ within a window of size N. 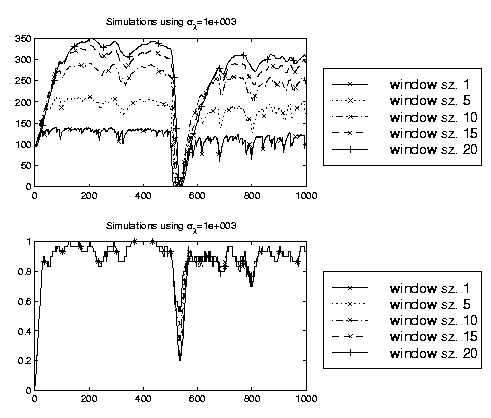The adaptive classifier requires to specify values for α, β and the window length N. Based on investigations with stationary data and with data with known non-stationary behavior we suggest to use α=0.01, β=10^-4 and N=10. Results on a synthetic data set with these and similar settings are shown in the figure on the left. The above plot illustrates the expectation of λ under the posterior. The second plot shows the instantaneous generalization accuracy. The data set is stationary - apart from a non-stationary behavior at sample 500, where we flip the labels. Although different values of N lead to different estimates of the optimal adaptation rate, the effect on the generalization accuracy is small and the best compromise between rapid tracking and high stationary accuracy is obtained with a window of size 10. As a final comment we would like to mention that these settings allow that the algorithm is done in real time - a vital property to be useful for a BCI.

References

(Beal et al. 2002)

M. J. Beal, H. Attias and N. Jojic. A Self-Calibrating Algorithm for Speaker Tracking Based on Audio-Visual Statistical Models. In Proc. Int. Conf. on Acoustics Speech and Signal Proc. (ICASSP), May 2002.

(Bernardo & Smith 1994)

J. M. Bernardo and A. F. M. Smith. Bayesian Theory. John Wiley & Sons, Chichester UK, 1994.

(Dellaportas & Stephens 1995)

P. Dellaportas and S. A. Stephens. Bayesian analysis of errors-in-variables regression models. Biometrics, 51:1085-1095, 1995.

(MacKay 1992)

D. J. C. MacKay. Bayesian interpolation. in Neural Computation, pages 415-447, 1992.

(Sykacek 1999)

Learning from uncertain and probably missing data. Peter Sykacek, OEFAI. An abstract is available on the workshop homepage.

(Sykacek et al. 2003 b)

P. Sykacek, I. Rezek and S. J. Roberts. Bayes Consistent Classification of EEG Data by Approximate Marginalisation. In S. J. Roberts and R. Dybowski editors. Applications of Probabilistic Models for Medical Informatics and Bioinformatics, pages to appear, Springer Verlag, 2003.

(Sykacek & Roberts 2003)

P. Sykacek and S. J. Roberts. Adaptive classification by variational Kalman filtering. In S.Thrun, S. Becker and K. Obermayer, editors, Advances in Neural Information Processing Systems 15, pp 737-744, MIT press, 2003.

(Sykacek & Roberts 2002)

P. Sykacek and S. Roberts. Bayesian time series classification. In T.G. Dietterich, S. Becker, and Z. Ghahramani, editors, Advances in Neural Processing Systems 14, pages 937–944. MIT Press, 2002.

(Wright 1999)

W. A. Wright. Bayesian approach to Neural-Network modeling with input uncertainty. IEEE Trans. Neural Networks, 10:1261-1270, 1999.

Brain computer interface

Brain computer interface summarizes all components necessary to establish a thought based human-computer communication channel. There are two main directions in BCI research. A BCI can be based on P300 related events with (Farwell & Donchin 1988) being one of the first references. The second class of BCI is based on voluntary control of cognitive tasks, with (Birbaumer et al. 1999) , (Pfurtscheller et al. 1993) and (Wolpaw et al. 1991) being the dominating research groups using this paradigm. Our BCI also follows this second line of thought. PARG members are involved in BCI research for about five years (Roberts et al. 1998). Having joined PARG and Oxford University in September 2000, I work on BCI since then.

BCI research in Oxford

In order to make our BCI simple to use, we record a few EEG channels only (four at most). Our recording equipment is based on a Gtec amplifier and an AD converter from national instruments. The low number of EEG channels requires the channel positions to be appropriately synchronized with the cortical area activated during the cognitive task under consideration. Thus our experimental protocol (Curan et al. 2003) requires input from cognitive psychology which in our case is provided by Prof. Stokes and her colleagues from the Research Department of the Royal Hospital for Neuro Disability, Putney, London. According to the taxonomy used in (Wolpaw et al. 2002), our research concentrates on the signal processing part of the BCI. In particular we regard the BCI as a feedback loop with two adaptive entities: on one hand the BCI user will adapt such as to maximize correct feedback; on the other hand machine learning techniques are inherently adaptive as well. The inevitable adaptation of the user requires signal processing concepts that can track non-stationary events. Thus the working hypothesis for our BCI 2003 is that it must use adaptive inference.

Probabilistic methods in BCI research

Probabilistic methods summarizes all approaches that are consistent with an axiomatic framework that result in Bayesian theory. Agreed - consistency is nice but from an application point of view, where performance is the only relevant measure, not necessary. However probabilistic methods have several other properties which make them extremely useful for many problems we encounter in the signal processing part of a BCI. To mention the most important:

• Model selection can be done consistently by using probabilistic methods. The true Bayesian approach (Sykacek 2000 b) would even go further and combine all models under consideration according to their probability under the training data. In the context of our BCI this has in (Curan et al. 2003) been applied successfully to find the optimal complexity of the BCI classifier.
• Probabilistic methods are inherently coupled with the concept of integrating out uncertainties (this refers to mathematical integration). In a multi sensor environment (e.g. multiple EEG channels) integration has the advantage to result in certainty based sensor fusion. Applied to BCI data (Sykacek & Roberts 2002 a) this leads to a significant improvement in bit rate. More detailed information on that issue is available on my machine learning research page in section Bayesian sensor fusion.
• A problem with non probabilistic BCI systems is that model fitting requires tuning of several parameters like penalty constants or model orders. Setting these parameters requires validation data and many time consuming repetitions of the model fitting process. The performance of the trained model depends critically on these parameters and requires expert knowledge. In a probabilistic world such parameters are called hyper parameters. The probabilistic framework provides means for inferring these hyper parameters together with model parameters in one go. Although we still have to choose some parameters, a well designed hierarchical setup makes inference less sensitive to their values. This aspect of probabilistic methods is of vital importance for our BCI research.

Alternative neuro-cognitive setup

In order to assess the effects on the bit rates of BCI's, we compare in (Curan et al. 2003) the communication bandwidth we may achieve with different cognitive tasks (Curran & Stokes 2003). We base comparisons on generalization accuracies obtained for independent test data. Differences are assessed for statistical significance using McNemar's test, a test for analyzing paired results that can be found in (Ripley 1996). In order to allow comparisons with other BCI systems, we also report bit rates as is suggested in (Wolpaw et al. 2000). The BCI experiments in this study were done by 10 young, healthy and untrained subjects. They are based on 3 cognitive tasks: an auditory imagination, an imagined spatial navigation task and an imagined right motor task. Each experiment consists of 10 repetitions of alternating pairs of these tasks each of which have been done for seven seconds. EEG recordings are obtained from two electrode sites: T4, P4 (right tempero-parietal for spatial and auditory tasks), C3' , C3" (left motor area for right motor imagination). The ground electrode is placed just lateral to the left mastoid process.

Comparing cognitive tasks.

comparison	accuracy (a)	bit/s (a)	accuracy (b)	bit/s (b)	Pnull
(a) vs. (b)	74 %	0.173	69 %	0.107	<<0.01
(a) vs. (c)	74 %	0.173	71 %	0.131	<0.01
(a) vs. (d)	74 %	0.173	71 %	0.131	0.01
(b) vs. (c)	69 %	0.107	71 %	0.131	0.02
(b) vs. (d)	69 %	0.107	71 %	0.131	0.03
(c) vs. (d)	71 %	0.131	71 %	0.131	0.40

An investigation of different classification paradigms reveals that on this data the BCI classifiers perform significantly better, when allowing for a nonlinear decision boundary. The method applied in this comparison uses autoregressive features (AR) extracted from successive segments of EEG. We use a generative classifier that predicts probabilities of cognitive states. Table Comparison of different tasks summarizes the results of this comparison. Task pairing (a) refers to the combination navigation - auditory, task pairing (b) refers to the combination navigation - right motor, task pairing (c) refers to the combination auditory - right motor and task pairing (d) refers to the combination left motor - right motor, which we include in order to allow for a comparison with these classical tasks. Our results allow to conclude that (a) vs. (b) result in slightly better correct classification rates as the classical imagined motor task. However, since we can extract information about the cognitive state in all cases, the main conclusion is that we might significantly increase the bit rate of BCI systems by using more than two cognitive tasks. For more details on this study we refer to (Curan et al. 2003).

Bayesian sensor fusion for offline BCI

Probabilistic models can be used to describe many architectures that have been applied to static and adaptive BCI systems. Examples are Hidden Markov models, that have been successfully applied to BCI in (Obermeier et al. 2001). Probabilistic models have also been quite popular tools in the machine learning and statistics community. Recently these communities have investigated efficient algorithms that allow inference of very complex models. These findings are of interest for the BCI community since they allow us to go beyond classical time series models and by that improve different aspects of BCI systems. We have recently evaluated two such generalizations in the context of BCI systems. Coupled HMM's are generalizations of ordinary HMM's, where two hidden state sequences are probabilistically coupled using arbitrary lags. In (Rezek et al. 2002) these models have been applied to movement planning and shown to outperform classical HMM's.

Another modification of HMM's was proposed in (Sykacek & Roberts 2002), where we follow probabilistic principles and suggest that classifications based on feature extraction (like the use of spectral representations or AR models as used in our BCI) have to regard the features as latent variables. Hence inference and predictions need to marginalize over this latent space. The practical advantage of the proposed architecture is that both the feature and the model uncertainty (the latter means the uncertainty about model order) are automatically taken into consideration. This effects model estimation and prediction and results in automatic artefact moderation and thus in intelligent sensor fusion. The idea exploits a property found by marginalization (i.e. integration over the distribution) over (at least two) uncertain latent variables estimated from two sensor signals (e.g. EEG recorded at different electrode sites). Depending on the variance of the distribution, we will obtain different posterior probabilities. Section Bayesian sensor fusion illustrates the effect using two sensor signals X_a and X_b and the state of interest (e.g. the cognitive state we want to predict) y. We see how the posterior probability depends on the variance. The effect may even result in a different assessment w.r.t. the predicted state.

The application of such a marginalization idea to BCI is illustrated in table BCI with fully Bayesian method. We illustrate results obtained with this paradigm using two task pairings of the study reported in our neuro-cognitive study. We compare the generalization accuracies of the fully probabilistic model (full Bayes) with those of a classical approach that does feature extraction separately. Table BCI with fully Bayesian method shows also the probabilities of the null hypothesis P_null that the results are equal (McNemar's test). We may thus conclude that a fully Bayesian approach significantly outperforms classifications obtained when conditioning on feature estimates. Despite having found that a fully Bayesian approach improves BCI performance, the proposed method has the disadvantage of not being directly applicable to online BCI. The computational complexity simply does not allow that. Hence we investigated an approximation which can be used in real time and nevertheless achieve the desired effects (Sykacek et al. 2003 b) .

BCI with fully Bayesian method.

	classical model		full Bayes
task pair	Accuracy	bit rate b/s	Accuracy	bit rate b/s	Pnull
(d)	75.9%	0.20	81.4%	0.31	0.04
(a)	76.2%	0.21	84.5%	0.38	<<0.01

Variational Kalman filter for adaptive BCI

Current BCI architectures developed by other research groups rely on assuming that the EEG generated during cognitive tasks shows stationary behavior. This assumption must be wrong for several reasons:

• There are technical problems with the electrolyte fluids used for electrode placement. It simply dries out and thus changes impedance. Hence both signal amplitudes and dynamics are subject to temporal variations during a BCI session.
• Both learning (habitation) effects and fatigue (Note at this point that sleep staging is entirely based on variations of EEG dynamics.) change the dynamics during and between BCI sessions.

We thus suggest a fully adaptive approach for the translation algorithm that, even in short time use of a BCI, resulted in higher communication bandwidth than conventional static BCI's. Probabilistic models can be of advantage in describing algorithms for adaptive BCI systems. A graph structure that illustrates such an approach is shown in my section on adaptive classification. We assume a model that predicts the probabilities of cognitive states and regard the parameters of the classifier are regarded as latent variables in a first order Markov process. The solution in a linear Gaussian case are the well known Kalman filter equations. In our case the non-linearity introduced by predicting probabilities requires us to use an approximation. We suggest for that purpose a variational technique and thus obtain variational Kalman filtering as an inference method (Sykacek & Roberts 2003) .

Variational methods (Jordan et al. 1999, Attias 1999) are attractive for BCI systems because compared with Laplace approximations (as e.g. used for classification problems in (Penny & Roberts 1999), they allow for more flexibility and contrary to particle filters they still provide a parametric form of the posterior. Having a parametric posterior is important since it allows efficient real time implementations. We apply this algorithm to features extracted from EEG. My favorite approach is to use a lattice filter representation of auto regressive parameters since they have in (Sykacek et al. 1999 c) been found superior to other feature extraction techniques including conventional AR parameters. Results applying the variational Kalman filter classifier to the BCI data described in our neuro-cognitive study, are summarized in table Adaptive BCI. The last column are the probabilities of the null hypothesis P_null that the results are equal (McNemar's test).The results suggest that a truly adaptive BCI (column vkf) significantly outperforms the equivalent static method (column vsi). A detailed description of our adaptive translation algorithm and a thorough evaluation can be found in (Sykacek et al. 2003 c).

Adaptive BCI.

	Generalization results
	vkf		vsi
Cognitive task	Accuracy	bit/s	Accuracy	bit/s	Pnull
navigation/auditory	86%	0.42	83%	0.34	0.02
navigation/movement	80%	0.28	80%	0.28	0.31
auditory/movement	78%	0.24	76%	0.21	<<0.01

Our BCI Publications

(Curran et al. 2003)

E. Curran, P. Sykacek, M. Stokes, S. J. Roberts, W. Penny, I. Johnsrude and A. M. Owen. Cognitive tasks for driving a Brain Compute Interfacing System. In IEEE Trans. Neural Systems and Rehabilitation Engineering, pages to appear, 2003.

(Sykacek 2003 b)

P. Sykacek. Brain Computer Interfacing: State of the Art, Probabilistic Advances and Future Perspectives. Technical Report, available in pdf and as gzipped postscript.

(Sykacek 2003 a)

P. Sykacek. Towards Adaptive BCI. Presentation at the NCAF meeting on human computer interaction, 3-4 September 2003, Cambridge, UK.

(Sykacek et al. 2003 c)

P. Sykacek, S. J. Roberts and M. Stokes. Adaptive BCI based on variational Bayesian Kalman filtering: an empirical evaluation. In IEEE Trans. Biomedical Engineering, pages to appear, 2003.
A poster describing the adaptive BCI was awarded in the "best engineering" category at the BCI workshop 2002 in Albany, NY, June 12-17.

(Sykacek et al. 2003 b)

P. Sykacek, I. Rezek and S. J. Roberts. Bayes Consistent Classification of EEG Data by Approximate Marginalisation. In S. J. Roberts and R. Dybowski editors. Applications of Probabilistic Models for Medical Informatics and Bioinformatics, pages to appear, Springer Verlag, 2003.

(Sykacek et al. 2003 a)

P. Sykacek, S. J. Roberts, M. Stokes, E. Curran, M. Gibbs and L. Pickup. Probabilistic methods in BCI research. In IEEE Trans. Neural Systems and Rehabilitation Engineering, pp. 192--195, 2003.

References

(Attias 1999)

H. Attias. Inferring parameters and structure of latent variable models by variational Bayes. in Proceedings of the Fifteenth Annual Conference on Uncertainty in Artificial Intelligence (UAI--99), pages 21-30, 1999.

(Birbaumer et al. 1999)

N. Birbaumer, N. Ghanayim, T. Hinterberger, I. Iversen, B. Kotchoubey, A. Kübler, J. Perelmouter, E. Taub and H. Flor. A spelling device for the paralysed. Nature , 398:297-298, 1999.

(Curran & Stokes 2003)

E. Curran and M. Stokes. Learning to control brain activity: A review of the production and control of EEG components for driving brain-computer interface (BCI) systems. Brain and Cognition, 51: 326–335, 2003.

(Farwell & Donchin 1988)

L. A. Farwell and E. Donchin. Talking off the top of your head: Toward a mental prosthesis utilizing event-related brain potentials. Electroencephalography and Clinical Neurophysiology , 70:510-523, 1988.

(Jordan et al. 1999)

M. I. Jordan, Z. Ghahramani, T. S. Jaakkola, and L. K. Saul. An introduction to variational methods for graphical models. In M. I. Jordan, editor, Learning in Graphical Models. MIT Press, Cambridge, MA, 1999.

(Obermeier et al. 2001)

B. Obermeier, C. Guger, C. Neuper, and G. Pfurtscheller. Hidden Markov models for online classification of single trial EEG. Pattern Recognition Letters, pages 1299–1309, 2001.

(Penny & Roberts 1999)

W. Penny and S. J. Roberts. Non stationary logistic regression. In Proceedings of the IJCNN 1999, 1999.

(Pfurtscheller et al. 1993)

G. Pfurtscheller, D. Flotzinger and J. Kalcher. Brain-Computer Interface - a new communication device for handicapped people. Journal of Microcomputer Applications , pages 293-299, 1993.

(Rezek et al. 2002)

I. Rezek, M. Gibbs, and S. Roberts. Maximum a posteriori estimation of coupled hidden Markov models. Advances in Neural Networks for Signal Processing, page to appear, 2002.

(Ripley 1996)

B. D. Ripley. Pattern Recognition and Neural Networks. Cambridge University Press, Cambridge, 1996.

(Roberts et al. 1998)

S. J. Roberts, W. Penny and I. Rezek. Temporal and Spatial Complexity Measures for EEG-based Brain-Computer Interfacing. Medical & Biological Engineering & Computing , 37(1), pages 93-99, 1998.

(Wolpaw et al. 1991)

J. R. Wolpaw, D. J. McFarland, D. J. Neat and C. A. Froneis. An EEG-based Brain-Computer Interface for Cursor Control. Electroencephalography and Clinical Neurophysiology , 78:252-259, 1991.

(Wolpaw et al. 2002)

J. R. Wolpaw, N. Birbaumer, D. J. McFarland, G. Pfurtscheller and T. M. Vaughan. Brain-computer interfaces for communication and control. Clinical Neurophysiology, 113:767-791, 2002.

(Wolpaw et al. 2000)

J. R. Wolpaw, N. Birbaumer, W. J. Heetderks, D. J. McFarland, P. H. Peckham, G. Schalk, E. Donchin, L. A. Quatrano, C. J. Robinson, and T. M. Vaughan. Brain-Computer Interface technology: a review of the first international meeting. IEEE Trans. Rehab. Eng., pages 164–173,2000.

Peter's SIESTA Page

This page is a summary of my SIESTA activities. I have looked at various aspects of the EEG model that should lead to the "core" sleep analyzer. These activities include deriving a Bayesian method for preprocessing, an investigation of resampling issues, Feature subset selection and an EEG model based on variational Bayesian techniques that forms the core of the SIESTA sleep analyzer. We decided for the Bayesian paradigm, since we found it extremely useful for automatic sleep classification according to Rechtschaffen & Kales rules (Sykacek et al. 1998 and Sykacek et al. 2002 a). I also came up with ideas how to combine models that were built separately for different biosignals. Below, we will use some acronyms: EEG - electroencephalogram (A signal obtained by recording from different positions on the scalp. It represents local brain activity.) EOG - electrooculogram (A signal recorded from the forehead that shows eye movements.) EMG - electromyogram (A signal recorded from various positions on the human body which represents the local muscle activity).

Bayesian preprocessing

The SIESTA analyzer processes EEG with a Bayesian implementation of an AR lattice filter structure. (Bayesian reflection coefficients). The difficulty with this representation is the calculation of the marginal likelihood of the model (i.e. integration of the distribution w.r.t. model parameters). Preprocessing results in a-posterior distributions of coefficients and posterior probabilities for models. Details have first been published in one of our EMBEC abstracts: (Sykacek et al. 1999 b) Based on this lattice filter model, I have also tried to obtain a REM/non REM feature from EMG. However this attempt failed - probably due to the same reasons why an amplitude based feature could not be derived.

Feature subset selection (FSS)

Since we wanted to make sure that the SIESTA analyzer is built around reasonable features, we decided to use feature subset selection techniques.

Conventional feature subset selection

FSS is the task of finding a sufficiently large best subset of features that should capture all details contained in some data relevant to a particular problem. This definition of FSS forces us to think about several issues:

1. What describes the relevant problem?
2. What is a proper measure of a "best" subset?
3. How do we determine whether a subset is sufficiently large?

We decided that the first question is best answered by considering how well subsets separate the corner stones of sleep (these are unambiguously classified segments of wake, deep sleep and REM sleep).

From a technical point of view there are several possibilities for measuring the quality of feature subsets. We decided to look at the likelihood function of various classifiers and a nonparametric estimate of an impurity measure (We measure the Gini index by a k nearest neighbors approach).

Search for the "best" subset was based on suboptimal algorithms (forward selection and sequential elimination). This was necessary since the number of features (more than 200) rendered exhaustive search impossible.

The optimal subset size was determined with a statistical significance test. We used McNemar's test of comparing two paired classifiers and an appropriate p-value. In the forward selection scheme we add the most promising feature if it increases the classification accuracy with statistical significance. In the backward elimination strategy, we remove the least important feature if it does not result in a statistically significant difference.

Classical FSS Results

As only 5 complete recordings were available until deadline for FSS, we could not use more than 4 recordings. (I saved one for validation purposes). A major problem in FSS was that the labels are given for 30 seconds segments and features are calculated on a one seconds basis. Different features were calculated on different explicitly or implicitly defined window lengths. As longer windows will smooth features, the 30 seconds labels will prefer such features that were calculated using longer windows. As reported in Den Haag, I could show this effect empirically. Consulting with S. Roberts, we came to the conclusion that it were best to use only the median sample of each 30 seconds segment. This should help reducing the effect of different window lengths.

The results in the following tables are from (Sykacek et al. 1999 c) .

Subset 1: Gini index and sequential forward selection

stochastic complexity at C3

Hjorth coefficient at Fp2: cmpl. /(act. * mob)

Subset 2: Likelihood of logistic regression
 

ref. coefficient at C4: 1st. coefficient

power spectral density at Fp1: Beta (12.5 Hz - 30.0 Hz)

Kalman AR coefficient at C3: 2nd. coefficient

A Bayesian wrapper

Conventional FSS has a major problem: If two or more (similar sized) subsets explain the problem equally well, using just one of them is in a Bayesian sense not consistent with the information provided. The correct approach would be to integrate out feature subset uncertainty. Consequently we also applied such a Bayesian technique to the problem of determining relevant feature subsets. The result of such FSS is a posterior probability over feature subsets. Prediction would then consider all subsets according to their posterior probability, which for the SIESTA data is shown in the image to the left. For further details of this method, I want to refer to my NIPS 99 preprint (Sykacek 2000 b).

Results Bayesian Wrapper

Subset 3: Bayesian wrapper for C3 only. The posterior probability of this subset is 0.69
 

ref. coefficient at C3: 1st. coefficient

ref. coefficient at C3: 3rd. coefficient

Hjorth coefficient at C3: cmpl. /(act. * mob)

The SIESTA sleep analyzer

The following considerations lead to the chosen architecture for the Siesta analyzer.

• Sleep should be modeled as a three state process (wake, REM and deep sleep). To capture uncertainty we model probabilities.
• Expert labels might disagree. In this case the independent variables should be used without label. This required a generative classifier and to model the joint density over the features extracted from EEG and the "sleep" state.
• We needed an inference scheme that allows for model selection (or model averaging) without being too difficult to compute on large data sets.
• Later extensions to include models from other sensors (e.g. an EMG model) should be relatively easy.

A generative model for classification

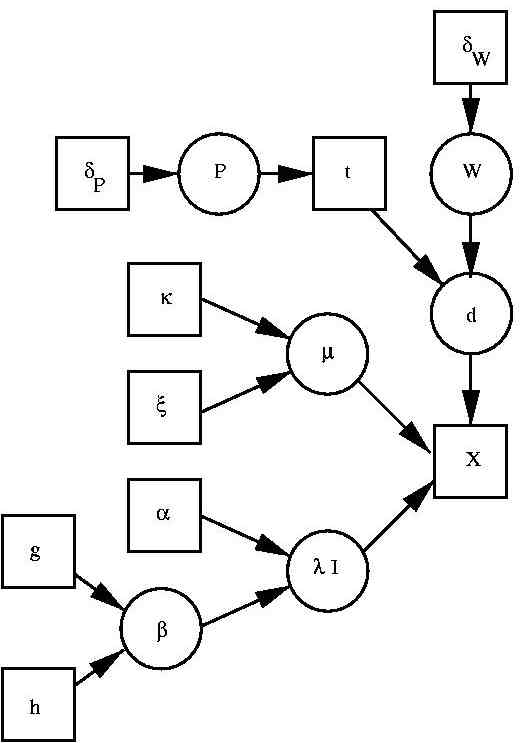We decided for a model that allows class conditional densities to be mixture of Gaussians. Together with prior probabilities for class, we thus have a generative model for EEG features that - via Bayes theorem - allows predicting probabilities for wake, REM and deep sleep. The corresponding graphical model is illustrated to the left. The basic architecture was previously used in a maximum likelihood setting e.g. (Trĺvén 1991). The architecture is a latent variable model consisting of the "features" x, the class label t and the kernel indicator d. In addition the Bayesian approach requires us to include all model parameters and hyper parameters as well. These are the prior probabilities of each class P and the parameters of the mixture model. For the latter we have W as (class conditional) kernel allocation probabilities, μ as kernel mean and λ as kernel precision (inverse kernel variance). The remaining variables specify a, partially hierarchical, prior which is largely influenced by (Richardson & Green 1997) . We have δ_P and δ_W as prior counts (we use 1) in the Dirichlet distributions over the corresponding variables P and W. Variables κ and ξ specify a Gaussian prior over the mean, μ. Variables α and β specify a Gamma prior over the kernel precisions, λ, where β is itself given a Gamma prior. This hierarchical setting is suggested by (Richardson & Green 1997) , to make inference less sensitive to the hyper parameter settings.

A Variational generative classifier

For reasons of computational efficiency we decided for a variational implementation for the generative classifier. The idea follows from implementations by (Attias 1999) who derives a variational solution for a Gaussian mixture model or (Gharamani & Beal 2000) who derives a variational implementation for a mixture of factor analyzers. Variational methods and the EM algorithm (Dempster et al. 1977) share the same ideas. The EM algorithm is a special case of a variational lower bound that becomes exact in the maximum. Unlike the EM, general variational algorithms remain a lower bound.

To obtain a lower bound, we apply Jensen's inequality, to the log marginal likelihood. In the simplest case we use a mean field assumption of a factorizing posterior distribution. Each circular variable in the DAG gets it's own approximate distribution. Details of how to derive the algorithm can be found in my PhD thesis (Sykacek 2000 a). As a result of iterating the variational updates to convergence we obtain a negative free energy for the model which can be used to guide model selection (Attias 1999). The plot to the right shows the negative free energies of a generative model for one of the electrodes (C3) for various numbers of Gaussian kernels. It suggests with very large probability a model with 15 kernels. More details on the prototype of the SIESTA sleep analyzer can be found in (Sykacek et al. 2001).

Results

If applied to new data, the SIESTA analyzer calculates probability traces that characterize the all-night sleep profile. An example plot is illustrated below.

References

(Attias 1999)

H. Attias. Inferring parameters and structure of latent variable models by variational Bayes. in Proceedings of the Fifteenth Annual Conference on Uncertainty in Artificial Intelligence (UAI--99), pages 21-30, 1999.

(Dempster et al. 1977)

A. P. Dempster, N. M. Laird and D. B. Rubin. Maximum likelihood from incomplete data via the EM algorithm (with discussion). In Journal of the Royal Statistical Society B, pages 1-38, 1977.

(Dorffner et al. 2000)

G. Dorffner, P. Sykacek, S. Roberts, A. Schlögl, A. Värri, P. Rappelsberger, P. Anderer, G. Klösch, B. Saletu, MJ. Barbanoj, W. Herrmann, S.-L. Himanen, B. Kemp, T. Penzel, J. Röschke. Continuous sleep processes and subjective sleep quality - first results from the SIESTA project. in J. Sleep Res Supplement 1., page 55, 2000.

(Flexer et al. 2002)

A. Flexer, G. Dorffner, P. Sykacek, I. Rezek. An automatic, continuous and probabilistic sleep stager based on a hidden Markov model. Applied Artificial Intelligence, 16(3):199-207,2002.

(Flexer et al. 2000)

A. Flexer, P. Sykacek, I. Rezek and G. Dorffner. Using hidden Markov models to build an automatic, continuous and probabilistic stager, in S. I. Amari et al., Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, IJCNN 2000, Como Italy, IEEE Computer Society, Vol. III, 627-631, 2000.

(Ghahramani and Beal 2002)

Z. Ghahramani and M. J. Beal. Variational inference for Bayesian mixture of factor analysers. Advances in Neural Information Processing Systems 12, 16(3):449-455, 2000.

(Kemp et al. 1998)

Kemp B, Penzel T, Värri A. O., Sykacek P., Roberts S. J.and Nielsen K. D. EDF: a simple format for graphical analysis results from polygraphic SIESTA recordings. in J. Sleep Research 7, suppl. 2, page 132, 1998.

(Richardson and Green 1997)

S. Richardson and P. J. Green. On Bayesian analysis of mixtures with an unknown number of components. in Journal Royal Stat. Soc. B, pages 731-792, 1997.

(Sykacek et al. 2002)

P. Sykacek, G. Dorffner, P. Rappelsberger and J. Zeitlhofer. Improving bio signal processing through modelling uncertainty: Bayes vs. non-Bayes in sleep staging. Applied Artificial Intelligence, 16(5):395-421,2002.

(Sykacek et al. 2001)

P. Sykacek, S. J. Roberts, I. Rezek, A. Flexer and G. Dorffner. A probabilistic approach to high resolution sleep analysis. In G. Dorffner, K. Hornik and H. Bischof, editors, Proceedings of the International Conference on Neural Networks (ICANN), pages 617-624, Springer Verlag, 2001.

(Sykacek 2000 b)

P. Sykacek. On input selection with reversible jump Markov chain Monte Carlo sampling. in S. A. Solla and T. K. Leen and K. R. Müller editors, Advances in Neural Information Processing Systems 12, pages 638-644, MIT press, 2000.

(Sykacek 2000 a)

P. Sykacek. Bayesian inference for reliable biomedical signal processing, PhD. thesis at the Technical University Vienna, defended in June 2000.

(Sykacek et al. 1999 c)

P. Sykacek, S. J. Roberts, I. Rezek, A. Flexer and G. Dorffner. Bayesian wrappers versus conventional filters: Feature subset selection in the Siesta project. in Proceedings of the European Medical & Biomedical Engineering Conference, pages 1652-1653, 1999.

(Sykacek et al. 1999 b)

P. Sykacek, S. J. Roberts, I. Rezek, A. Flexer and G. Dorffner. Reliability in preprocessing: Bayes rules Siesta. in Proceedings of the European Medical & Biomedical Engineering Conference, pages 1656--1657, 1999.

(Sykacek et al. 1999 a)

P. Sykacek, S. J. Roberts, I. Rezek, A. Flexer and G. Dorffner. Classification in the sampling paradigm: A predictive approach towards a Siesta sleep analyzer in Proceedings of the European Medical & Biomedical Engineering Conference, pages 1660-1661, 1999.

(Sykacek et al. 1998)

P. Sykacek, G. Dorffner, P. Rappelsberger and J. Zeitlhofer. Experiences with Bayesian learning in a real world application. in M. I. Jordan and M.J. Kearns and S. Solla editors, Advances in Neural Information Processing Systems 10, pages 964-970, 1998.

(Sykacek et al. 1997)

P. Sykacek, G. Dorffner, O. Filz, P. Rappelsberger and J. Zeitlhofer. Classification of REM sleep periods with artificial neural networks. in Proc. of Measurement '97, (Smolenice, 1997), pages 327-333, 1997.

(Trĺvén 1991)

H. G. C. Trĺvén. A neural network approach to statistical pattern classification by ``semiparametric'' estimation of probability density functions in IEEE Trans. Neural Networks, pages 366-377, 1991.

Online Supplement to “Bayesian Modelling of Shared Gene Function”

This work was done by the authors, while contributing to the BBSRC funded "Shared Genetic Pathways in Cell Number Control" research program, which was awarded to the Department of Pathology, University of Cambridge, UK. As the project title suggests, this project investigates molecular biological processes that control development cycles in different biological systems. The search for the underlying genetic markers requires a principled approach that can infer which genes are of shared importance in several microarray experiments. We propose for that purpose a fully Bayesian model for an analysis of shared gene function. The approach assumes that several microarray experiments with known cross annotations between transcripts (genes) should be analyzed for common genetic markers. The implementation described in this work has in particular the advantage to combine data sets before applying thresholds and thus the advantage that the result is independent of that choice. For more information on the method, we refer to the original paper (Sykacek et al 2007 a) and the pdf supplement (Sykacek et al 2007 b).

Experimental Supplement

Biological Details

The analysis of development processes in many tissues is faced with several interacting biological processes and a mix of various cell types. As an example we investigate in this work the shared biological activity at gene level in a mouse mammary gland development cycle (Clarkson et al 2004) and a human endothelial cell culture with apoptosis induced by serum withdrawal (Johnson et al 2004). The biological complexity of the experiments is best visualized, if we mark different development stages for active biological processes at a macro level. For the mouse mammary time course, we get the following table of active processes. During lactation, time is in days and during involution we use hours.

Biological Processes During Lactation and Involution in Mouse Mammary Development

Biological Process	L0	L5	L10	I12	I24	I48	I72	I96
Type I Apoptosis	-	-	-	+	+	?	-	-
Type II Apoptosis	-	-	-	-	-	?	+	+
Apoptosis	-	-	-	+	+	+	+	+
Differentiation	+	+	+	?	-	-	-	-
Inflammation	?	-	-	+	+	?	-	-
Remodeling	-/(?)	-	-	-	-	?	+	+
Acute Phase	+	-	-	-	+	+	+	+

We use "+" to indicate that a process is active and "-" to indicate it's inactivity. A "?" indicates epochs where we are uncertain about the process activity. A similar though simpler classification can be obtained for the second experiment which studies human endothelial cells under serum deprivation. Duration during serum deprivation is in hours.

Biological Processes in Endothelial Cells Under Serum Withdraw

Biological Process	control (t0)	t28
Type II Apoptosis	-	+
Apoptosis	-	+
Differentiation	+	-

Results

In addition to the results we present in the original paper and in the pdf supplement, we provide here the top 20 genes we find important to contribute to both data sets.

Ranking From Shared Analysis of Mammary Development and Endothelial Cells

Gene Symbol	P(It|D)	P(G=t|D)	Co-Regulation
SAT	0.99951	0.047597	anti
ODC1	0.99921	0.029237	co
GRN	0.99921	0.029125	co
BSCL2	0.99919	0.028601	anti
MLF2	0.99884	0.019988	anti
IFRD2	0.99867	0.017425	co
BTG2	0.99843	0.014688	co
CCNG2	0.99826	0.013274	co
TNK2	0.99789	0.010943	anti
C9orf10	0.99783	0.010614	co
HAGH	0.99764	0.0097747	co
PPP2CB	0.99759	0.0095567	anti
SSR1	0.99748	0.0091528	co
MUT	0.99747	0.0091039	co
DHRS3	0.99746	0.0090926	co
PSMA1	0.99741	0.0089018	anti
HBLD2	0.99732	0.0086073	co
SYPL1	0.99724	0.0083639	co
C2F	0.99723	0.0083374	co
ATP6V1B2	0.99706	0.0078419	anti

The full gene list in comma separated format is available as zipped archive. To check, which biological processes we find attributed to this list, we follow the suggestion in (Lewin et al. 2006) and use Fishers exact test to infer significance levels of active gene ontology (GO) categories from the probabilistic rank list (see also (Al-Shahrour et al.)). The resulting GO categories for the gene list of this shared analysis can be obtained as comb_apo_all.xml in xml format. This file is compatible with Treemap - (C) University of Maryland and preserves the parents - child relationships from the directed acyclic GO graph. Note that the treeml.dtd file is part of the Treemap package and not available here. Treemap is under a non commercial license. If it is unavailable despite that, the xml file can be inspected with any reasonable web browser.

Software

The software to calculate indicator probabilities that capture shared gene function comes as collection of MatLab libraries. The package consists of the main code, which uses the variational Bayesian approach described in (Sykacek et al 2007 a) and additional functions for data handling, output generation and an EM implementation for regularized probit link regression used during initialization of all Q-distributions. To make the software distribution flexible, all MatLab functions are collected in archives each containing functions of a particular type. The software is available under GPL 2 license and comes without any warranty.

Installation

To install the package, one has to download all required archives, provided as *.zip files or tared gzip archives (*.tar.gz), unpack the archives and set appropriate MatLab paths. Scripts using a hypothetical experiment derived from a mouse testis time course kindly provided by R. Furlong, demonstrate how to use the library.

Library Files for Shared Analysis (Zip files ending with .zip instead of .tar.gz are available as well)

Library File	Description
helpers.tar.gz	generic helper functions
statsgen.tar.gz	generic statistics functions
mca_base.tar.gz	basic microarray file handling (loading various microarray data formats)
mca_fuse.tar.gz	generic handling in connection with shared analysis (cross annotation and output generation)
probitem.tar.gz	Penalized maximum likelihood (MAP) for probit link regression via an EM algorithm.
combanalysis.glb.hphp.tar.gz	Variational Bayes for shared analysis of subset probabilities in probit regression.

All components required to successfully run the experiment, will be installed automatically, if one creates a new directory and then downloads and runs the setup script in that directory. Linux (Unix) users should use combsyssetup.sh. After download, you might have to set executable permission by invoking the command chmod +x combsyssetup.sh. Windows users should either do the same after installing a cygwin environment or install the Wget and Unzip packages from GnuWin32 and then download and run combsyssetup.bat Note that this will install all required packages and, if run at later times, install updates.

Tutorial

After having run the script, the installation directory contains MatLab scripts and data which illustrate the approach discussed in (Sykacek et al 2007 a). The data are extracted from a subset of a mouse testis development time course, kindly provided by R. Furlong. The data consists of 7 time points: adult day 1 day 5 day 10 day 15 day 23 and day 35, with differential expression measured against the adult generation.

Data Files for the Tutorial

To illustrate all steps from cross annotation to generation of gene lists, we divided this data artificially into two "experiments". One experiment contains the samples of the adult generation and days 1 and 15. Here we use the original gene ids. We assume that the biological state change is between adult and the other two development periods. The corresponding data file is called "exp1mca.tsv" and is formatted like FSPMA normalized raw output: Gene ids are used as column headers and all samples as rows below. We also have a corresponding effects description as "exp1eff.tsv", which is used to generate the labels. The second experiment contains days 35, 23, 5 and 10 and artificially modified gene ids, to mimic a situation that requires between species annotation. Here we assume that the biological states correspond to days 35 and 23 versus days 5 and 10. The files are "exp2mca.tsv" for the microarray data and "exp2eff.tsv" for the labels. Note that the assumption is that each experiment provides information about differences in late and early stages of testis development. The analysis goal is thus similar to a problem, where we attempt to combine two experiments obtained from different platforms or species. This requires "cross annotation", which is here done according to the tab delimited file "crossann.tsv". In general, each row in this file contains a tuple that provides a unique mapping between all different unique gene ids one finds in a shared analysis. To complete the list of files, we provide in addition the tab delimited file "genespec.csv", which provides for the unique gene ids in the target genome, a mapping to gene symbols and descriptions.

Data Files - Summary Table

File Name	Description
exp1mca.tsv, exp2mca.tsv	Normalized log ratios (location and scale adjustment)
exp1eff.tsv, exp2eff.tsv	(default) Labels
crossann.tsv	cross annotations between the different gene ids found in the gene lists
genespec.csv	mapping from unique gene ids (for the cross annotation target) to standardized symbols and gene descriptions
shareanalysis.def	specification of the cross annotated experiments that enter shared analysis

Matlab Scripts for the Tutorial

Script files, to be run in the order as listed in the table.

File Name	Description
crossann.m	cross annotation of microarray experiments and preparation of shared analysis
runsim.m, calccoreg.m	calculation of gene indicator probabilities of shared gene function by variational Bayesian inference
combres2csv.m	extraction of gene ranking w.r.t. shared gene function as a tab delimited file

Both artificial experiments have to be cross annotated. This step will align the gene ids in different experiments and provide two raw data files and a gene id to symbols and description annotation in MatLab 6 format. Cross annotation is done by the MatLab script crossann.m found in the installation folder.

After cross annotation, we have to prepare for the shared analysis. This requires to specify a tab delimited text file ("shareanalysis.def") which controls this process. The minimal requirement is to specify in this control file which (previously cross annotated) data files should be analyzed for shared gene function. In addition one can specify a different set of labels. This is useful to analyze the same data for different biological classifications. We may also provide independent test data, which will be used to obtain generalization errors. Analysis is stared with the script combanalysis.m in the installation folder. The simulation will, depending on the size of the problem and the mode of analysis, take up to several hours (this example is though done in less than one minute or in a few minutes time, if we want fold results). As a result we get all simulation output in MatLab format. Details of the calculated results require to look into the code and to analyze the variables stored in the MatLab output file.

The last step in an analysis of shared function is to generate a rank table of shared gene function. This is done with the script crossann2csv.m found in this folder as well. The result is a rank list of similar structure as the one provided in the supplement of the original paper.

All intermediate results generated during a shared analysis is stored in MatLab 6 format (for Octave compatibility). The final rank table is a comma separated file.

Summary of result files as generated from this simulation.

File Name	Description
exp1.mat, exp2.mat	cross annotated and normalized raw data
crossanngenespec.mat	reordered gene specifications (id, symbol and description)
state.mat, crosslog.mat	internal log files (see code)
sharetestres.mat	inference result about shared gene function. This file contains all results including probabilities, predictions and all Q-distributions found from variational Bayesian inference.
share_test_rank.csv	rank table as comma separated file.

Adapting Shared Analysis to Different Experiments

To run such an analysis on a different experiment, one must provide data files structured like those listed in the data files table. The structure of the microarray data and the default labels is identical to the output generated by FSPMA, which can thus be used as preprocessing tool. In addition, one has to generate a file which allows cross annotation between all gene sets that appear in any one data set. If there is only one set of gene ids, cross annotation should be done anyway, to obtain the data in the format as expected by runsim.m. In this case all parts in runsim.m that specify the shared analysis will refer to the same gene id column. Inference of shared gene function requires in addition a control file similar to shareanalysis.def. Finally one has to adjust all script files in the script files summary to meet the different requirements.

Acknowledgments

This page describes joint work with R. Clarkson, C. Print, R. Furlong and G. Micklem. We also thank David MacKay for advise. The project was moslty done at the Departments of Pathology and Genetics, University of Cambridge as part of the project "Shared Genetic Pathways in Cell Number Control", ref. 8/EGH16106 funded by the BBSRC within their Exploiting Genomics initiative. During completion of this work, Peter Sykacek moved to the Bioinformatics group at BOKU University, Vienna, which is funded by the WWTF, ACBT, Baxter AG, and ARC Seibersdorf.

References

(Al-Shahrour et al.)

F. Al-Shahrour, R. Díaz-Uriarte, and J. Dopazo. FatiGO: A web tool for finding significant associations of Gene Ontology terms with groups of genes. in Bioinformatics, 20, pages 578--580, 2004.

(Attias 1999)

H. Attias. Inferring parameters and structure of latent variable models by variational Bayes. in Proceedings of the Fifteenth Annual Conference on Uncertainty in Artificial Intelligence (UAI--99), pages 21-30, 1999.

(Clarkson et al 2004)

R. W. E. Clarkson, M. T. Wayland, J. Lee, T. Freeman and C. J. Watson. Gene expression profiling of mammary gland development reveals putative roles for death receptors and immune mediators in post-lactational regression. in Breast Cancer Res., 6(2), pages 92--109, 2004.

(Johnson et al 2004)

N. A. Johnson, S. Sengupta, S. A. Saidi, K. Lessan, S. D. Charnock-Jones, L. Scott, R. Stephens, T. C. Freeman, B. D. Tom, M. Harris, G. Denyer, M. Sundaram, S. K. Smith and C. G. Print. Endothelial cells preparing to die by apoptosis initiate a program of transcriptome and glycome regulation. in The FASEB Journal, 18, pages 188--190, 2004.

(Lewin et al. 2006)

A. Lewin, S. Richardson, C. Marshall, A. Glazier, and T. Aitman. Bayesian Modelling of Differential Gene Expression. in Biometrics,62(1), pages 10--18.

(Sykacek et al. 2007:a)

P. Sykacek, R. Clarkson, C. Print, R. Furlong and G. Micklem. Bayesian Modeling of Shared Gene Function. In Bioinformatics, 2007; doi: 10.1093/bioinformatics/btm280, pp 1936--1944. An abstract and a pdf preprint are available from Bioinformatics online, a local draft version is draft available in gzipped postscript and pdf.

(Sykacek et al. 2007:b)

P. Sykacek, R. Clarkson, C. Print, R. Furlong, and G. Micklem. Supplement to:"Bayesian Modeling of Shared Gene Function". Technical report, Department of Biotechnology, BOKU University, Vienna, 2007, available in gzipped postscript and pdf.